במהלך השבוע האחרון שאלו אותי כמה אנשים שאני מלווה על מונחים סטטיסטיים לדאטה אנליסט שדרשו מהם להכיר בראיונות עבודה.
לאור השאלות, החלטתי לכתוב מאמר חדש בנושא מונחים סטטיסטיים לדאטה אנליסט, על מנת שיהיה קל יותר להבין את הבסיס בתחום – גם אם לא למדתם סטטיסטיקה באוניברסיטה.
במהלך המאמר נדבר על 6 המונחים הסטטיסטיים הבאים:
- שדות קטגוריאליים/ רציפים
- חציון ואחוזונים
- התפלגות נורמלית
- קורלציה
- סיבתיות
- מובהקות סטטיסטית
אז בלי יותר מדי חפירות – בואו נתחיל!
מונח א' – שדות קטגוריאליים / רציפים
כשאנחנו באים לנתח דאטה, חשוב קודם כל להבין מהו סוג המשתנה שאנחנו מנתחים.
קיימים 2 סוגים עיקריים של שדות: קטגוריאליים ורציפים.
שדות רציפים הם המקרה הפשוט: אלו מדדים/מספרים, שניתן לשים אותם על סקאלה כלשהי, ולבצע בהם את פעולות החישוב המתמטיות שאנחנו מכירים: חיבור, חיסור, כפל, חילוק וכיו"ב.
שדות קטגוריאליים כוללים ערכים שאינם מספריים, או ערכים מספריים שאינם רציפים – לרוב ערכים טקסטואליים או טווחים של מספרים.
מדוע חשוב להבחין בין השדות? כי מדדים מסוימים אפשריים רק בחלקם.
לדוג': רשימה של 3 הערכים השכיחים ביותר לא רלוונטית בשדות רציפים, ממוצע לא ניתן להפעיל על שדות טקסט או טווחים (כמו "מיהי המדינה הממוצעת…" או "מהו ממוצע טווח הגילאים")…
מונח ב': חציון + אחוזון
לפני שנצלול למונח החציון, בואו נתחיל "לחמם מנועים" עם מונח בסיסי בעולם הנתונים: ממוצע.
ממוצע הוא מדד, אשר בא לסכם בצורה פשוטה סדרת ערכים/תצפיות לכדי ערך אחד בלבד, והוא תוצאה של חישוב סכום הערכים בסדרת התצפיות, לחלק במספר התצפיות.
באותה הצורה, קיים מדד נוסף שמטרתו דומה – והוא החציון.
חציון הוא הערך, שחצי מהתצפיות בסדרה קטנות ממנו, וחצי גדולות ממנו.
מה ההבדל בין חציון וממוצע?
ובכן, במקרים רבים מקובל להשוות את החציון לממוצע, ומשם לזהות תופעות מעניינות בנתונים.
בפרמטרים, שבהם קיימים ערכים קיצוניים – הערך הממוצע עשוי להיות מוטה.
בואו ניקח לדוגמה את רמת השכר במשק.
נניח שנרצה למדוד את רמת השכר על פני זמן, ולזהות מגמות.
המדד הראשון שנבחן יהיה כמובן השכר הממוצע.
הבעיה היא, שהשכר הממוצע במשק עשוי להיות מוטה ע"י שכירים המרוויחים סכומים מאוד גבוהים – נניח מעל למיליון ש"ח לשנה.
אז אמנם ישנם יחסית מעט אנשים כאלה, אבל עצם השכר הגבוה שלהם יגדיל מאוד את הממוצע, וזה לא תמיד ייצג נאמנה את רמת השכר (כי רוב האנשים ירוויחו כ-100-200 א' ש"ח, ולא מיליון).
ולכן, מקובל להשתמש בחציון.
כאמור, השכר החציוני יתאר את השכר ש-50% מהשכירים ירוויחו יותר ממנו, ו-50% ירוויחו פחות ממנו.
ומאחר ואחוז האנשים שמרוויחים משכורת מאוד גבוהה הוא נמוך למדי (אחוזים בודדים), השכר שלהם ישפיע הרבה פחות על ערך החציון מאשר על הממוצע.
כך, כאשר נשווה את השכר החציוני למול השכר הממוצע, נקבל כמעט תמיד שהממוצע גדול יותר (מוטה מעלה).
בדיוק באותה הצורה שבה נחשב את החציון, ניתן לחשב גם אחוזונים – כלומר הערך שבו אחוז מסוים באוכלוסייה יהיה מעל לאותו הערך – והיתר מתחת.
לדוג': העשירון העליון במשק הוא השכר ש-10% מהאוכלוסייה ירוויחו מעליו, ו-90% מהאוכלוסייה ירוויחו מתחתיו, המאיון העליון הוא הערך של 1% מהאוכלוסייה שמרוויחים הכי הרבה וכיו"ב.
התכונה הזו של ממוצע למול החציון או אחוזונים – יכולה לתת לנו מידע בסיסי אך חשוב לגבי צורת ההתפלגות של השדה שאנו בודקים, ולכן חשוב להכיר אותה.
מונח ג' – התפלגות נורמלית
 במהלך החיים כנראה שרובנו חווינו את האמירה "את/ה לא נורמלי/ת!!!".
במהלך החיים כנראה שרובנו חווינו את האמירה "את/ה לא נורמלי/ת!!!".
אבל ככל הנראה, שמי שאמר לנו את זה לא באמת הבין את המשמעות הסטטיסטית של המושג הזה…
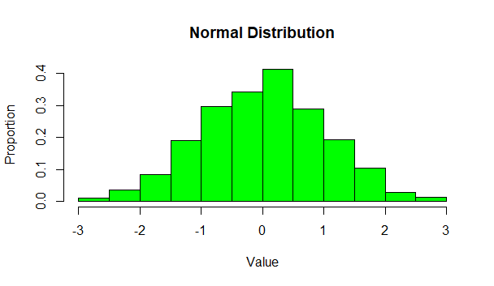
אז מהי התפלגות נורמלית?
ובכן, מדובר בצורת התפלגות, המתארת תופעות "נורמליות", שבהן תופעה מסוימת תהיה מאוד שכיחה סביב ערך מסוים, והרבה פחות שכיחה ככל שנתרחק מאותו הערך.
לדוג': משקל או גובה.
נניח שנלך ברחוב, ונגיד שלום ל-100 גברים טיפוסיים – האם סביר שאחוז גדול מהם יהיה במשקל 75 ק"ג או במשקל 125 ק"ג? ואולי במשקל 50 ק"ג?
ובכן, ברור ש-75 ק"ג.
מדוע? מאחר ואנחנו שייכים לזן מסוים, יש לנו מכנה משותף – מעין "תבנית" או "ספר הפעלה".
הזן שלנו נוצר (בהערכה גסה, לצורך הדוגמה) עם משקל שכיח של כ-70-80 ק"ג לגברים, וכ-55-65 לנשים;
או עם גובה שכיח של סביב 1.70-1.80 לגברים, וכ-1.50-1.60 לנשים (שוב, בהערכה גסה).
כלומר – קיים ממוצע מסוים לכל אוכלוסייה.
בנוסף, כל אחת ואחד מאיתנו הם ייחודיים, כלומר שונים במעט מהאחרים.
ההיבט הזה, של השונות – מתנהג בצורה מסוימת במשקל והגובה:
הרבה מאיתנו יהיו קרובים מאוד לממוצע, ומעט מאיתנו יהיו הרבה מעל או מתחת לממוצע.
הצורה הזו של ההתפלגות נקראת "נורמלית" או "פעמון", ובשפה המתמטית הצורה נקראת "גאוסיאן" (על שם המתמטיקאי "גאוס").
מונח ד' – קורלציה – Correlation
מונחים סטטיסטיים לדאטה אנליסט כוללים לא רק תופעות או מדדים הקשורים למשתנה בודד מסוים, ולכן החל מעכשיו אנחנו מתחילים לדבר על קשר בין מספר משתנים.
קורלציה (או מתאם) היא בעצם רמת ההתאמה של ערכי 2 שדות למגמה מונוטונית, או במילים אחרות:
האם ערכי שדה א' וערכי שדה ב' הולכים באותו הכיוון?
לדוג': משקל וגובה מתואמים אחד לשני – ככל שהגובה גדול יותר בקרב אוכלוסייה מסוימת, כך גם המשקל יהיה גדול יותר.
כמובן שיהיו מקרים שבהם אדם ששוקל 80 ק"ג יהיה גבוה יותר מאדם השוקל 100 ק"ג, אבל עבור כלל האוכלוסייה ההיפך יהיה הנכון.
קורלציה בין 2 משתנים יכולה להיות או חיובית או שלילית (מתאם הפוך):
חיובית: ככל שערכי שדה א' גדלים גם ערכי שדה ב' גדלים – כמו משקל וגובה;
שלילית: ככל שערכי שדה א' גדלים – ערכי שדה ב' דווקא יקטנו – כמו גיל ורמת הדופק המקסימלי.
קורלציה תהיה לרוב אחד המדדים הראשונים והחזקים ביותר שלנו כאנליסטים לטובת גילוי תובנות מעניינות הנוגעות לקשר בין שני משתנים בדאטה.
מונח ה' – סיבתיות – Causality
בעוד שקורלציה באה לתאר התאמה כללית בין שני משתנים, כשלעצמה היא לא תמיד תגיד הרבה.
מדוע?
בואו נניח לרגע שאנחנו עובדים בפייסבוק.
נניח, שזה עתה גילינו שמשתמשים חדשים שהוסיפו 10 חברים תוך שבוע מההצטרפות שלהם הם בעלי 90% סיכוי להמשיך ולהשתמש בכלי;
ושמי שהוסיפו רק 3 חברים בשבוע הראשון ימשיכו רק ב-20%.
המשמעות היא, שאם נעודד את כל המשתמשים להוסיף לפחות 10 חברים – נוכל לפתור כמעט לחלוטין את הבעיה של משתמשים חדשים שמצטרפים ונוטשים.
זה שווה את ערכו בזהב לחברה, כי זיהינו תופעה מסוימת (הוספת X חברים) שמשפיעה על תופעה אחרת (המשך שימוש בכלי)!
לכן, המטרה האולטימטיבית שלנו כאנליסטים היא לזהות קשרים של סיבה ותוצאה בין השדות בדאטה – כלומר איך שדה א' משפיע על שדה ב'.
זה נקרא סיבתיות (Causality).
סיבתיות נבדלת מקורלציה בדיוק בזיהוי המשתנה האחד המשפיע על המשתנה השני, בצורה כזו שנוכל לשנות את ערך המשתנה הראשון – ולגרום לשינוי בערך המשתנה השני.
אגב, חשוב לציין שלא תמיד תהיה סיבתיות כזו.
לדוג': המשקל והגובה לא כוללים קשר שאחד מהם משפיע על השני.
הרי את הגובה אנחנו לא ממש יכולים לשנות (נעזוב לרגע אפשרות של ניתוח השתלת גובה…), ואם נוריד במשקל הגובה לא ממש ישתנה…
לכן, העקרון הוא לזהות קורלציה בין 2 משתנים – ולאחר מכן להבין מהו המשתנה שנוכל להשפיע דרכו על המשתנה השני.
מונח ו' – מובהקות סטטיסטית – Statistically significance
המובהקות הסטטיסטית היא אחד המונחים החשובים ביותר בעולם האנליטי – ולא בכדי;
היא בעצם מה שמבדיל בין ממצא "רגיל" או "מהבטן" לממצע מדעי – המגובה במדד כמותי תומך.
בדוגמה הקודמת של פייסבוק, "מצאנו" שמתוך המשתמשים שהוסיפו 10 חברים בשבוע הראשון שלהם המשיכו ב-90% להשתמש בכלי, ומתוך המשתמשים שהוסיפו רק 3 חברים – 80% נטשו (20% המשיכו).
לכאורה ממצא מאוד מעניין.
אבל עכשיו נוסיף עוד נתון לתמונה:
נניח שהממצא הזה מתבסס על 20 משתמשים חדשים בלבד: 10 שהוסיפו 10 חברים, ו-10 נוספים שהוסיפו 3 חברים.
עכשיו נשאלת השאלה: האם התובנה אכן נכונה, בהתבסס על 20 משתמשים בלבד?!
הרי 20 תצפיות זה מספר מאוד נמוך, וייתכן שהוא רגיש מדי לטעויות או אקראיות.
בדיוק לצורך הזה נועדה בדיקת המובהות הסטטיסטית.
המובהקות הסטטיסטית בעצם נותנת לנו אינדיקציה כמותית לשאלה האם הממצא שזיהינו בקורלציה/ סיבתיות/וכו' נובע מסיבה אקראית מסוימת, או שהוא חזק יותר מטעויות אקראיות כאלו?
לרוב, היקף תצפיות נמוך בדאטה יצביע על אקראיות בתוצאות, בעוד שהיקף תצפיות גדול יעיד על רמת אקראיות נמוכה – ולכן רמת סבירות גבוהה שהממצא אכן מובהק סטטיסטית.
ובנוסף, חשוב מאוד להדגיש שמובהקות סטטיסטית היא רק מדד כמותי המחזק את הממצא שזיהינו – והוא עדיין יכול להיות לא נכון!
לדוג': אחת מהבעיות הכי גדולות עם עולם ה-Big Data, היא שכאשר יש לנו כ"כ הרבה דאטה, תמיד נוכל למצוא בו Subset (מדגם) שבו נזהה כל ממצא העולה על הדעת – גם אם נשמע הזוי לחלוטין…
ישנו את הסיפור המפורסם של המטוסים במלחמת העולם השניה, שחזרו עם חורים של קליעים ממטוסי אויב, ולכן חשבו לחזק את המקומות עם החורים.
שם, אמנם היתה מובהקות סטטיסית במיקום החורים, אבל גם היתה הטיה בעלת משמעויות דרמטיות:
הניתוח התבצע רק על מטוסים שחזרו בשלום!
ובעוד שהמיקום שבו לא היו חורים לכאורה העיד על כך שמטוסי האויב לא יורים לשם –
בפועל המטוסים שנורו במיקום הזה פשוט לא חזרו!!
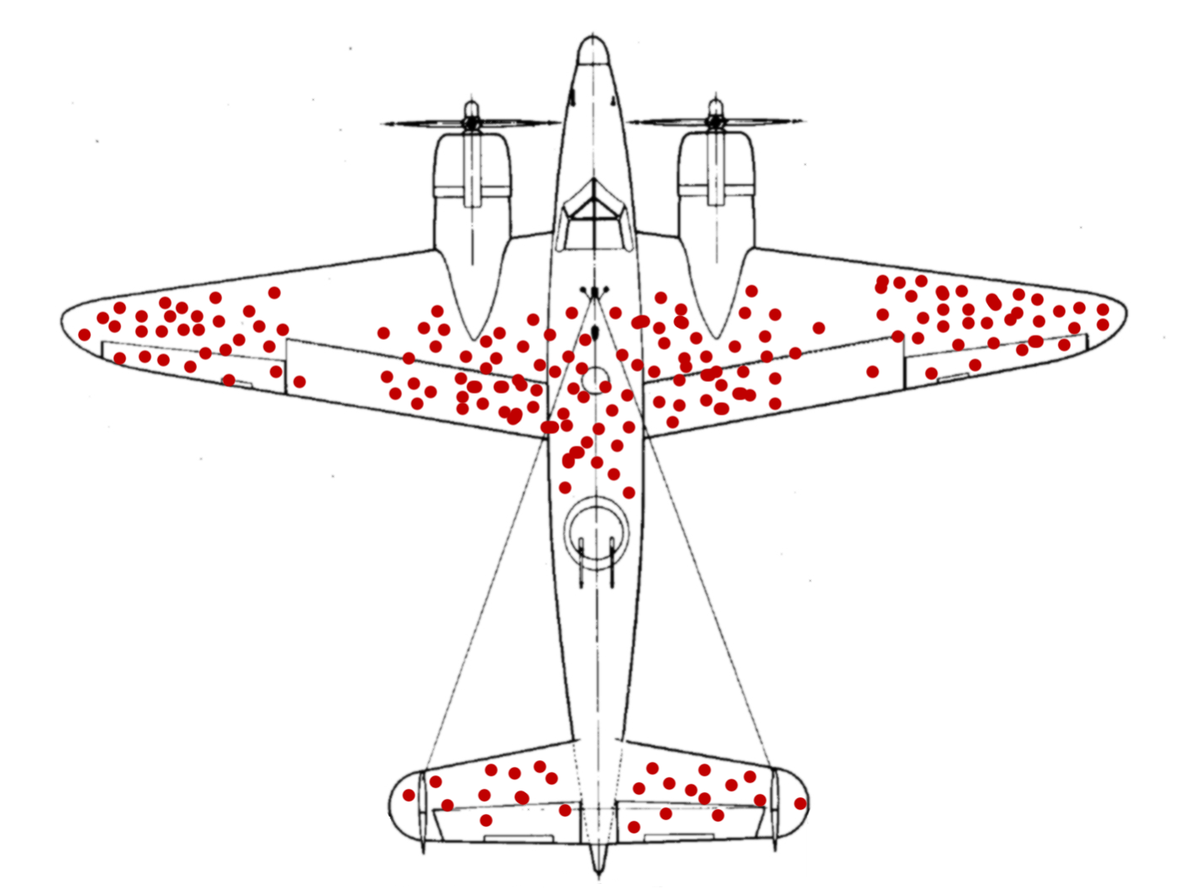
By McGeddon – Own work, CC BY-SA 4.0, Link
סיכום
במסגרת המאמר עברנו בצורה בסיסית על מספר מונחים סטטיסטיים לדאטה אנליסט שחשוב שנכיר – לפחות בתחילת הדרך.
מאחר וידע סטטיסטי הוא אחד הכלים החזקים ביותר שיש לנו כאנליסטים על מנת לנתח דאטה ולזהות מגמות ותובנות בעלות משמעות – מומלץ מאוד להעמיק בתחום וללמוד אותו – גם ברמה הטכנית וגם ברמה המתודולוגית.
זה יסייע לנו גם לתת עוד חיזוק כמותי לממצאים שלנו, וגם יאפשר לנו להגיע לתובנות חדשות לחלוטין, היכולות לשפר באופן משמעותי את ביצועי החברה או הארגון שלנו.
אז בפעם הבאה שיתקילו אתכם עם המונחים "מובהקות סטטיסטית", "התפלגויות", "קורלציה" ושאר קללות ביידיש – אני מקווה שתבינו על מה מדובר.
בהצלחה!
